"Закон природы включает в рассмотрение важнейший элемент- ритмичность. Закон природы - это не некая система, не метод игры на рынке, а явление, характерное, видимо, для хода любой человеческой деятельности. Его применение в прогнозировании революционно."

Эллиотт

История “Золотого сечения” - это история человеческого познания мира. Понятие “Золотое сечение” прошло в своем развитии все стадии познания. Первая ступень познания открытие “золотого сечения” древними пифагорейцами. От простого созерцания действительности они перешли к выражению его в мире чисел, но ими были спутаны причинно-следственные понятия мира и догадка о мировой значимости “Золотого сечения” осталась лишь догадкой на века. И все же, в своей жизнедеятельности человек начинает использовать “Золотое сечение” в своих художественных произведениях.

Вся древнегреческая культура развивалась под знаком золотой пропорции. Греки первые установили: пропорции хорошо сложенного человеческого тела подчиняются ее законам, что особенно хорошо видно на примере античных статуй (Аполлон Бельведерский, Венера Милосская). Фригийские гробницы и античный Парфенон, театр Диониса в Афинах - все они исполнены гармонии золотой пропорции. В наши дни интерес к золотой пропорции возрос с новой силой. В целом ряде музыковедческих работ подчеркивается наличие золотого сечения в композиции произведений Баха, Шопена, Бетховена.

В эпоху Ренессанса золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи, Рафаэль, Микеланджело, Тициан и другие великие художники возрождения компонуют свои полотна, сознательно используя золотую пропорцию. Нидерландский композитор XV века Якоб Обрехт широко использует “Золотое сечение” в своих музыкальных композициях, которые до сих пор уподобляют “кафедральному собору”, созданному гениальным архитектором.

Практические нужды торговли подводят Фибоначчи к открытию своих рядов, которые еще никто не связывает с “Золотым сечением”. В XIX веке уже не художники, а ученые-экспериментаторы, изучавшие закономерности филлатаксиса (расположение цветков), вновь обратились к золотой пропорции. Оказалось, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках и т. д. “упакованы” по логарифмическим спиралям, завивающимся навстречу друг другу. При этом числа “правых” и “левых” спиралей всегда относятся друг к другу, как соседние числа Фибоначчи (13:8, 21:13, 34:21, 55:34), предел последовательности которых является золотая пропорция.

Ученые открывают “Золотые пропорции” в живой и не живой материи и уже на основании этого опыта происходят удивительные открытия нашими современниками Стаховым А. П. и Витенько И. В. Обобщенных золотых пропорций и обобщенных рядов Фибоначчи. Их анализ приводит исследователей к результатам ошеломляющим по своей простоте и от того более значительных: “Золотое сечение” обладает избыточностью и устойчивостью, которые позволяют организовываться самоорганизующимся системам.

Тема работы: золотое сечение - основа структурной гармонии природных и искусственных систем. Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Цель работы доказать, что принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Для полного раскрытия темы автор должен рассмотреть следующие темы:

1) Что такое золотое сечение? Какова его связь с рядом Фибоначчи?

2) Выяснение общих закономерностей развития живой и неживой природы.

3) Найти математические закономерности в пропорциях тела человека.

4) Рассмотреть действие закона золотой пропорции в физическом и биологическом мире.

5) Установить общие фундаментальные закономерности в развитии Земли как органически цельной системы.

6) Рассмотреть исторический процесс в соответствии с законами роста «по Фибоначчи»

7) Золотое сечение как критерий гармонии и красоты в природе, искусстве, архитектуре и.т.д.

Ответы на вопросы автор нашел в еженедельном учебно-методическом приложении к газете «Первое сентября» Математика, в книгах Волошинова В.А. , ВоробьеваН.Н., Стахова А. П, Ковалева Ф.В. Для более глубокого изучения данной темы автор работы вынужден был прибегнуть к Интернет – технологиям.

Глава 1. «Золотое сечение» в математике

1.1. «Золотое сечение» – гармоническая пропорция

«Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое – деление отрезка в крайнем и среднем отношении. Первое можно назвать мерой золота, вотрое же больше напоминает драгоценный камень»

Кеплер

В математике пропорцией (лат. proportio) называют равенство двух отношений:

a : b = c : d.

Отрезок прямой АВ можно разделить на две части следующими способами:

на две равные части – АВ : АС = АВ : ВС;

на две неравные части в любом отношении (такие части пропорции не образуют);

таким образом, когда АВ : АС = АС : ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.

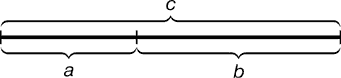
Рис. 1. Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

Построение деления отрезка в золотой пропорции.

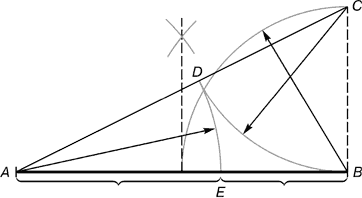
Рис. 2. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки B восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Доказательство:

Из DABC по теореме Пифагора имеем: AC²= AB²+ CB², так как AC= AD + DC то
(AD + DC)² = AB²+ CB²,

по построению AD = AE, DC = CB= ½ AB.

Из этих равенств следует (AE + ½ AB)² = AB² + AB²/4

AE²+ AE*AB=AB²

Разделим обе части равенства на АЕ*АВ:

АВ –АЕ = ЕВ => отсюда следует, что точка Е – золотое сечение отрезка АВ.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x² – x – 1 = 0.

Решение этого уравнения:

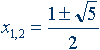
Число j, называемое золотым сечением, входит в тройку самых известных иррациональных чисел, то есть таких чисел, десятичные представления которых бесконечны и непериодичны. Остальные два вы конечно знаете: это p – отношение длины окружности к диаметру и е – основание натуральных логарифмов

Чему же равно j? Напомним определение: большая часть относится к меньшей как все к большей. Если меньший отрезок принять за единицу, то можно записать пропорцию: ( Х+1 ) / Х = Х / 1, которая сводится к обычному квадратному уравнению Х²-Х-1=0. Это число одновременно выражает длину отрезка Х и значение величины j. Его десятичное разложение имеет вид 1,61803398.

Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.

Для построения пентаграммы необходимо построить правильный пятиугольник. Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Построение «золотого» прямоугольника:

Построим квадрат ABCD со стороной a. Найдем середину М отрезка АВ. Проведем дугу окружности с центром в М радиуса МС, до пересечения с продолжением стороны АВ в точке Е. Закончим построение прямоугольника AEFD.

Доказательство:

По теореме Пифагора из DМСВ: МС² = МВ² + ВС² = (а/2)² + а ² = а²

МЕ =МС по построению, тогда АЕ=АМ+МЕ= + а = а

Следовательно, АЕ= AD,

А М В Е

D C F

1.2. Ряд Фибоначчи

"Любой человеческой деятельности присущи три отличительных особенности: форма, время и отношение, -и все они подчиняются суммационной последовательности Фибоначчи".

Эллиотт

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Месяцы	0	1	2	3	4	5	6	7	8	9	10	11	12	и т.д.
Пары кроликов	0	1	1	2	3	5	8	13	21	34	55	89	144	и т.д.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Глава 2. Периодичность в истории

2.1. Периоды жизни человека

Давно замечено, что жизнь человека протекает неравномерно. В ней четко прослеживается периодичность различных процессов, наличие переломных и кризисных моментов, качественных скачков. При этом периодичность жизненного процесса не может быть сведена к движению по кругу, когда мы все время возвращаемся к исходной точки, а скорее всего напоминает движение по спирали, когда как будто происходит также возвращение, но каждый раз на новом уровне.

"Фибоначчиева" закономерность прослеживается уже при эмбриональном развитии ребенка, которое завершается в нормальных условиях на 266-е сутки после оплодотворения яйцеклетки. График роста массы эмбриона в зависимости от возраста имеет несколько изломов, соответствующих примерно 24, 100, 200 суткам. Эти изломы характеризуют различные фазы перестройки в развитии эмбриона. В возрасте 24 сутки происходит переход от клеточного развития к организменным механизмам регуляции; в возрасте примерно 100 суток заканчивается период перестройки и наступает фаза устойчивого развития организма эмбриона; на 200-е сутки завершается формирование всех органов ребенка и рождение ребенка после этого срока не исключает его дальнейшего нормального развития.

Рассмотрим, как можно выразить через золотую пропорцию все указанные критические точки в развитии эмбриона. Если число 266 (период эмбрионального развития ребенка) разделить на квадрат золотой пропорции, то получим число 101,6, которое соответствует критической точке 100 суток. Если число 101,6 разделить на куб золотой пропорции, то получим число 24, которое соответствует еще одной критической точке в развитии эмбриона (24 суток). Наконец, интервал 266 - 101,6 = 164,4, деленный золотой пропорцией, дает число 202,6, что соответствует третьей критической точке 200 суток. Критические возрасты мужчин соответствуют следующим годам: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, а вся жизнь мужчины делится на 7 периодов: до года - младенчество, 1-8 лет - детство, 8-13 - отрочество, 13-21 - юность, 21-34 - молодость, 34 - 55 лет - зрелость, 55-89 - старость.

Семь отрезков времени - это семь различных жизней, которые дает человеку природа. Они различны по физическому времени, то есть по числу оборотов Земли вокруг своей оси: первый этап длится один год, а последний (55-89 лет) - 34 года. Но биологическое время для этих этапов одинаково, но первый этап (до одного года) длится биологически столько же, сколько и последний (от 55 до 89 лет). Биологическое время отражает скорость различных процессов, протекающих в организме. В процессе старения организма скорость метаболических процессов в нем снижается. Поэтому и возникает ощущение, что с возрастом "время бежит быстрее" - ведь человек оценивает время не биологически, а физически. Вывод о замедлении собственного биологического времени и ускорении физического времени человека при старении подтвержден экспериментами. Доказано, например, что с увеличением возраста скорость заживления ран снижается и с возрастом уставший от работы человек медленнее восстанавливает свои силы.

Белорусский философ Эдуард Сорокко высказывает предположение, что "фибоначчиевый" характер развития присущ не только организму человека, но и "всем самоорганизующимся системам. Это относится к организмам животных, популяциям, экологическим сообществам и даже социальным системам. Сорокко делает предположение, что исторический процесс социальных формаций развертывается во времени в соответствии с законами роста "по Фибоначчи", переходя от "детства" к "отрочеству", "юности", "зрелости" и т.д. И если организм человека в своем развитии переживает качественные скачки - "эпицентры физиологических революций", то подобные скачки должны прослеживаться и в развитии общественных формаций.

2.2.Последовательность Фибоначчи и хронология древнейшей истории.

В качестве инструмента хронологии впервые была избрана гармоническая система числовых отношений, так называемый ряд Фибоначчи Приведем ее начальную часть:1, 1, 2, 3, 5, 8 и т. д.

Приметы такого ряда очевидны в хронологии эпох I тыс. н. э. - I тыс. до н. э. Числа ряда удачно фиксируют поздний железный век(I тыс. н. э.) и начало железного века(I тыс до н.э.). В интервале 5 - 2 тыс. до н. э. сосредоточены культуры энеолита, ранней и поздней бронзы Европы, к интервалу 8 - 5 тыс. до н. э. относят европейский мезолит и неолитические культуры Ближнего Востока. Правда, мезолит Ближнего Востока датируют иначе: 10 - 7 тыс. до н.э., а мезолит Восточной Европы - 11 - 6 тыс. до н. э. Особенности в хронологии культур 10 - 5 тыс. до н. э. региональны. Они зависят от неравномерности развития, которая возникла в верхнем палеолите и сохранялась на протяжении всего времени в дальнейшем.

Замеченные расхождения в хронологии археологических эпох имеют региональный масштаб, никак не затрагивают самой числовой последовательности, присущей ряду Фибоначчи: 1, 1, 2, 3, 5, 8. Очевидно, что в хронологии археологических культур более раннего времени, развитию которых присущ планетарный характер, следует ожидать более строгого соответствия ряду Фибоначчи. Продолжим ряд, его составляют такие числа: 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1 597, 2 584, 4181 и т.д.

Cначала казалось удивительным: некоторые элементы этой последовательности, действительно, соответствуют хронологическим рубежам в древнейшей истории.Так, позицию 233 тыс. лет в приводимой последовательности можно отождествить с датой рисского оледенения в Европе, общепризнанная геологическая дата которого 230 тыс. лет т. н. Позиция, соответствующая 377 тыс. лет, близка дате в 400 тыс. лет т. н. этому времени относят выход человечества из биоценоза.

Около середины II миллионолетия (1 597 тыс. л., согласно ряду) складывается древнейшая археологическая культура Олдувай, в середине III миллионолетия (2 584 тыс. лет) появляются австралопитековые формы ископаемого человека, с которым связывают так называемое начало орудийности. На протяжении 720 - 600 тыс. лет складывается трудовая традиция и формируется речь. Дата завершения этих процессов находится почти рядом с позицией ряда в 610 тыс. лет.

Действительно, эти рубежи разграничивают развитие человечества на отдельные этапы, которые иногда называют временными ступенями. Переход с одной временной ступени на другую считают эволюцией системы. Повторим ряд, обозначив курсивом те ступени, хронология которых проверена: 1, 1, 2, 3,5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610, 987,1 597, 2584 .

Одиннадцать из 18 позиций ряда проверены и подтверждены с достаточной степенью надежности и точности. Иногда говорят, что одно подтверждение - случайность, два - совпадение, три - тенденция. В нашем случае не три, а 60% совпадений проверены и подтверждены. Такое число подтверждений можно считать выражением не столько тенденции, сколько закономерности.

Итак, хронология и периодизация, можно сказать, исторического развития с помощью ряда Фибоначчи разделена на 18 временных ступеней, имеющих планетарный характер. Повторим их 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1 597, 2 584. В основе такого выбора лежит научное мировоззрение, которое всегда строго и определенно. Таковы, в первом приближении, возможности использования ряда Фибоначчи в разработке периодизации и общей хронологии развития человечества с древнейших времени до начала современной эпохи.

Глава 3. Самоорганизация неживой природы

3.1.Оптимальные физические параметры внешней среды

Органы чувств человека дают ему возможность воспринимать все многообразие внешнего мира, чутко реагировать даже на незначительные изменения внешней среды, выбирать способ поведения, обеспечивающий ему безопасное для жизни существование. Однако органы чувств не могут воспринимать весь диапазон соответствующих параметров внешней среды, которые могут возникнуть в природе. Существуют некоторые границы ощущения, характеризуемые минимальными и максимальными параметрами внешней среды, которые человек способен воспринимать. Эти границы называются абсолютно нижним и абсолютно верхним порогами ощущений.

В книге русского ученого В.И. Коробко "Золотая пропорция и проблемы гармонии систем" (1998 г.) предпринята интересная попытка показать, что нижние и верхние пороги связаны через золотую пропорцию.

Громкость звука. Известно, что максимальная громкость звука, которая вызывает болевые ощущения, равна 130 децибелам. Если разделить этот интервал золотой пропорцией 1,618, то получим 80 децибел, которые характерны для громкости человеческого крика. Если теперь 80 децибел разделить золотой пропорцией, то получим 50 децибел, что соответствует громкости человеческой речи. Наконец, если разделить 50 децибел квадратом золотой пропорции 2,618, то получим 20 децибел, что соответствует шепоту человека. Таким образом, все характерные параметры громкости звука взаимосвязаны через золотую пропорцию.

Влажность воздуха. При температуре 18-20° интервал влажности 40-60% считается оптимальным. Границы оптимального диапазона влажности могут быть получены, если абсолютную влажность 100% дважды разделить золотым сечением:

100/2,618 = 38,2% (нижняя граница); 100/1,618 = 61,8% (верхняя граница).

Давление воздуха. При давлении воздуха 0,5 МПа у человека возникают неприятные ощущения, ухудшается его физическая и психологическая деятельность. При давлении 0,3 - 0,35 МПа разрешается только кратковременная работа, а при давлении 0,2 МПа разрешается работать не более 8 мин. Все эти характерные параметры связаны между собой золотой пропорцией:

0,5/1,618 = 0,31 МПа; 0,5/2,618 = 0,19 МПа.

Температура наружного воздуха. Граничными параметрами температуры наружного воздуха, в пределах которых возможно нормальное существование (а, главное, стало возможным происхождение) человека является диапазон температур от 0 до +(57-58)°С. Разделим указанный диапазон положительных температур золотым сечением. При этом получим две границы:

Обе границы являются характерными для организма человека температурами: первая соответствует температуре тела человека 36,6°С, вторая является наиболее благоприятной температурой для организма человека. Последнюю границу можно получить из температуры тела человека с помощью золотой пропорции: 36,6/1,618 = 22,62°С.

Хотя все эти расчеты, на первый взгляд, кажутся искусственными, но тем не менее они заставляют нас задуматься над ними, а иногда и практически использовать.

3.2. Симфония Земли

Космическое тело под названием Земля в процессе глобальной самоорганизации превратилось в "Прекрасную Симфонию", основанную на "золотом сечении".

Начнем из соотношения суши и воды на поверхности Земли. Оказывается, что площадь океанов близка к 62%, остальная поверхность планеты занята материками и морями. Случайно ли, что отношение этих двух основных образований, определяющих вид планеты, рельеф земной коры и ее сложную геоморфологическую жизнь, отвечает золотой пропорции? Очевидно, нет. За длительный период эволюции, длившийся около 4,5 миллиарда лет, структура планеты должна была достичь некоторого оптимального состояния. И эта гармония выразилась в том, что, с одной стороны, Земля превратилась в геододекаэдр, а с другой стороны, соотношение суши и воды на ее поверхности стало равным отношению золотой пропорции.

Как в теле человека кровь осуществляет перенос веществ по всему организму, обеспечивая обмен веществ, создание новых структур, выведение шлаков, так разветвленная система водных артерий производит перенос веществ на планете, питание растений, очистку почв, перенос веществ. Солнечный насос, как сердце, перегоняет воду, поднимая ее с поверхности океана в атмосферу, и затем орошает дождем поверхность биосферы. Вся система водоснабжения - от просачивания воды по капиллярам почвы и пропитывание пород, до образования мелких ручейков, речушек и громадных водных артерий - разве все это не напоминает кровеносную систему человека и других высших организмов Земли

Начнем с состава воздуха. Если бы в воздухе Земли было 25% кислорода, а не 21, как сейчас, то лес мог бы гореть под дождем, считают ученые. А если бы кислорода было бы всего 10%, то не горела бы даже сухая древесина. Похоже, что 21% кислорода в нынешней атмосфере величина не случайная, а результат жизнедеятельности биосферы, итог самоорганизации планеты.

Земная кора сложена горными породами осадочного и магматического происхождения. За долгую историю Земли происходило образование разнообразных магматических пород. Среди разнообразных разновидностей пород преобладают две группы - кислые (граниты, гранодиориты) и основные (габбаро, бальзаты), остальные встречаются в десятых долях процента. 61% послекембрийских пород составляют кислые, а 38,5% - основные породы. Для магматических пород всех возрастов кислые породы составляют 62,2 %, а основные - 34,7%. Отношение содержания кислых пород к основным равно 1,6 для докембрийских пород и 1,66 для послекембрийских. В пределах точности все эти соотношения отвечают золотой пропорции! Не здесь ли проявляется основной принцип построения земной коры, основанный на гармоническом соотношении кислых и основных магматических пород? Возникает вопрос: является ли образование магматических пород "игрой случая" или подчинено некоторой фундаментальной закономерности, "стремлению" к гармонической, наиболее целесообразной организации?

Выяснение общих фундаментальных закономерностей развития Земли как космического тела только начинается. Сейчас актуальной задачей является объединение знаний, создание общей науки о Земле как органически цельной системы и важную роль в создании науки о Земле могут сыграть закономерности золотого сечения.

Глава 4. Принципы формообразования в природе

4.1. Самоорганизация живой природы

Все, что приобретало какую-то форму на Земле, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах- рост вверх или расстилание по поверхности земли и закручивание по спирали. И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы- симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Как подчеркивает Н. Васютинский в своей книге "Золотая пропорция", "рост "по Фибоначчи" открыл большие возможности для возникновения разнообразных организмов. В членении "по Фибоначчи" выражена и геометрическая прогрессия роста (с показателем, равным золотой пропорции), и симметрии подобия, и единство непрерывной и дискретной организации. В процессе эволюции происходило усложнение организмов, что вызывало увеличение количества частей тела и костей в скелете. Этот процесс осуществлялся не только непрерывно, но и дискретно, следуя некоторому "плану эволюции по Фибоначчи". На смену примитивным моллюскам пришли более сложные организмы и, прежде всего, членистоногие".

Членение "по Фибоначчи" весьма распространено среди различных типов животных, включая членистоногих, насекомых, черепах и высших животных. В процессе эволюции тело членистоногих разделилось на три отдела: головной, грудной и брюшной. Среди современных членистоногих можно назвать следующих характерных представителей: мечехвост, имеющий 5 пар конечностей, 5 пар шипов на брюшке, 5 сегментов на груди; лангуст, имеющий также 5 пар ног, 5 перьев на хвосте, каждая нога состоит из 5 частей, а брюшко из 5 сегментов. У скорпионов туловище состоит из двух частей - брюшка и хвоста. Они имеют 5 пар конечностей, на брюшке выделяются 8 сегментов, на хвосте - 5. Напомним, что 5 и 8 - числа Фибоначчи.

Большой интерес представляет исследование форм птичьих яиц. Их всевозможные формы колеблются между двумя крайними типами: один из них может быть вписан в прямоугольник золотого сечения, другой - в прямоугольник с модулем

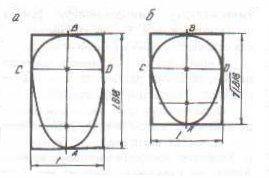
Такие формы птичьих яиц не являются случайными, поскольку в настоящее время установлено, что форме яиц, описываемых отношением золотого сечения, отвечают более высокие прочностные характеристики оболочки яйца.

Таким образом, золотое сечение, числа Фибоначчи и пентагональная симметрия являются бесспорным элементом роста живых существ.

4.2.Золотые спирали и "пентагональная" симметрия в живой природе

"Золотые" спирали широко распространены в биологическом мире. Этот рост осуществляется по логарифмической спирали. В книге "Кривые линии в жизни" Т. Кук исследует различные виды спиралей, проявляющихся в рогах баранов, коз, антилоп и других рогатых животных. Среди множества спиралей он выбирает "золотую" спираль ("кривую гармонического возрастания") и рассматривает ее как символ эволюции и возрастания.

Спирали широко проявляют себя в живой природе. Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно, в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровне.

Форма раковин поражает своим совершенством и экономичностью средств, затраченных на ее создание. Идея спирали в раковинах выражена не приближенно, а в совершенной геометрической форме, в удивительно красивой, "отточенной" конструкции

У некоторых моллюсков количество частей, формирующих конические раковины, отвечает числам Фибоначчи. Так, раковины фораминифер имеют 13 частей, раковины шпорцевой улитки - 8, количество камер раковины наутилуса - 34, тело наутилоидей делится на 13 частей, раковина гигантской тридакны собрана в 5 складок. Число ребер ископаемой раковины брахиопод равно 34. Такое же количество ребер имеют крохотные раковины тектакулитов. По краям пятнистой раковины ципреи из Индийского океана расположены мелкие зубцы, количество которых равно 21. Из приведенных примеров видно, что конструкции раковин многих ископаемых и современных моллюсков предпочитают числа 5, 8, 13, 21, 34.

Но еще более убедительной демонстрацией проявления золотого сечения в мире растений является явление "филлотаксиса"

4.3.Филотаксис

Все в Природе подчинено строгим математическим законам. Оказывается, что расположение листьев на стеблях также носит строгий математический характер и это явление называется в ботанике "филлотаксисом". Суть филлотаксиса состоит в винтовом расположении листьев на стебле растений (ветвей на деревьях, лепестков в соцветьях и т.д.).

В явлении филлотаксиса используются более сложные понятия симметрии, в частности понятие "винтовая ось симметрии". Рассмотрим, например, расположение листьев на стебле растения. Мы видим, что листья находятся на различных высотах стебля вдоль винтовой линии, обвивающейся вокруг его поверхности. Для того чтобы перейти от нижележащего листа к следующему, приходится мысленно повернуть лист на некоторый угол вокруг вертикальной оси стебля, а затем поднять его на определенный отрезок вверх. В этом и состоит суть "винтовой симметрии".

Ботаники утверждают, что дроби, характеризующие винтовые оси растений, образуют строгую математическую последовательность, состоящую из отношений соседних чисел Фибоначчи, то есть:

1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, ... .

(1)

Вспомним, что ряд Фибоначчи есть следующая последовательность чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... .

(2)

Сравнивая (1) и (2) нетрудно увидеть, что дроби в последовательности (1) образуются числами Фибоначчи, взятыми через одно число.

Ботаники установили, что для различных растений характерны свои дроби филлотаксиса из последовательности (1). Например, дробь 1/2 свойственна злакам, березе, винограду; 1/3 - осоке, тюльпану, ольхе; 2/5 - груше, смородине, сливе; 3/8 - капусте, редьке, льну; 5/13 - ели, жасмину и т.д. Какова же "физическая" причина, лежащая в основе "законов филлотаксиса"? Ответ очень прост. Оказывается, что именно при таком расположении листьев достигается максимум притока солнечной энергии к растению.

С учетом этого замечания нас теперь не удивит и тот факт, что практически все соцветья и плотно упакованные ботанические структуры (сосновые и кедровые шишки, ананасы, кактусы, головки подсолнечников и многие другие) также строго следуют числам Фибоначчи.

Таким образом, строгую математику мы находим и в расположении лепестков на цветке розы и в разрезе яблока (пентаграмма), и в сосновой шишке, и в головке подсолнечника. И мы снова и снова убеждаемся в том, что все в природе подчинено единому плану, единым законам - и раскрыть и объяснить эти законы и есть главная задача человеческой науки.

4.4.Ритмы сердца и мозга

Сердце бьется непрерывно - от рождения человека до его смерти. И его работа должна быть оптимальной, обусловленной законами самоорганизации биологических систем. А так как золотая пропорция является одним из критериев самоорганизации в живой природе, естественно было предположить, что и в работе сердца возможно проявление этого критерия. Эта гипотеза и лежит в основе исследований сердечной деятельности млекопитающих, проведенных русским биологом В.Д. Цветковым.

Равномерно бьется сердце человека - около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает, а затем выталкивает кровь и гонит ее по телу. Давление крови изменяется в процессе работы сердца. Наибольшей величины оно достигает в левом желудочке сердца в момент его сжатия (систолы). В артериях во время систолы желудочков сердца кровяное давление достигает максимальной величины, равной 115-125 мм ртутного столбца у молодого, здорового человека. В момент расслабления сердечной мышцы (диастола) давление уменьшается до 70-80 мм рт.ст. Отношение максимального (систолического) к минимальному (диастолическому) давлению равно в среднем 1,6, то есть близко к золотой пропорции. Случайное ли это совпадение или закономерное, отражающее гармоническую организацию сердечной деятельности?

На кардиограмме сердца выделяется два участка различной длительности, соответствующие систолической (t₁) и диастолической (t₂) деятельности сердца. В.Д. Цветков установил, что у человека и у других млекопитающих имеется оптимальная ("золотая") частота сердцебиения, при которой длительности систолы, диастолы и полного сердечного цикла (T) соотносятся в пропорции золотого сечения, то есть T : t₂ = t₂ : t₁. Так например, для человека эта "золотая" частота равна 63 ударам сердца в минуту, для собак - 94, что отвечает реальной частоте сердцебиения в состоянии покоя.

Приведенные выше примеры, подтверждающие действие закона золотой пропорции в физиологических ритмах и функциях организма человека хорошо иллюстрируют взаимосвязь явлений и процессов физического и биологического миров с общим законом пропорциональности в природе.

Глава 5.Формула красоты

"Созерцая совершенное, прекрасное человеческое лицо и тело, невольно приходишь к мысли о каком-то скрытом, но явственно чувствующемся математическом изяществе его форм, о математической правильности и совершенстве составляющих его криволинейных поверхностей!"

Уже тысячелетия люди пытаются найти математические закономерности в пропорциях тела человека, прежде всего человека хорошо сложенного, гармоничного. На протяжении многих веков отдельные части тела человека служили единицами длины. Так, у древних египтян было три единицы длины: локоть (466 мм), который равнялся семи ладоням (66,5 мм), ладонь, в свою очередь равнялась четырем пальцам. Основными мерами длины в России были сажень и локоть, связанные с ростом человека; кроме того, применялся дюйм - длина сустава большого пальца, пядь - расстояние раздвинутых большого и указательного пальцев, ладонь - ширина кисти руки.

Еще в Древнем Египте за единицу измерения тела принимали длину стопы. При этом высота человека составляла в среднем 7 длин его стопы. В соответствии с эстетическим каноном греческого скульптора Поликлета единицей измерения тела служила голова; длина тела должна быть равной восьми размеров головы.

Золотая пропорция занимает ведущее место в художественных канонах Леонардо да Винчи и Дюрера. В соответствии с этими канонами золотая пропорция отвечает не только делению тела на две неравные части линией талии. Высота лица (до корней волос) относится к вертикальному расстоянию между дугами бровей и нижней частью подбородка, как расстояние между нижней частью носа и нижней частью подбородка относится к расстоянию между углами губ и нижней частью подбородка, это отношение равно золотой пропорции.

Займемся теперь "инвентаризацией" человеческого тела. У него одно туловище, одна голова, одно сердце и т.д.; многие части тела парные, например, рук, ноги, глаза почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. У человека 12 пар ребер (одна пара атрофирована и присутствует в виде рудимента). Очевидно в прошлом у человека было 13 ребер, но в процессе эволюции, при переходе к прямостоячему положению количество ребер уменьшилось.

Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют числа Фибоначчи от 1 до 34. Заметим, что общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.

Но фибоначчиева закономерность характерна не только для костей. Например, в строении головного мозга различают семь частей: кора, мозолистое тело, мозжечок, мозговой желудочек, моси, продолговатый мозг, гипофиз. В основании головного мозга выделяют 8 частей, выполняющих разные функции. В теле человека насчитывается 8 различных желез внутренней секреции. Кишечник и соседние с ним органы (желудок, печень, желчный пузырь и т.д.) составляют в сумме 13 органов. Дыхательные органы человека состоят из 8 частей. Печень также состоит из 8 частей; почки состоят из 5 частей, а сердце из 13.

Этот список частей человека, в перечне которых обнаруживаются числа Фибоначчи, можно было бы продолжить. Случайно ли это? Скорее всего - нет. Человек, как и другие творения природы, подчиняется всеобщим законам развития. Корни этих законов нужно искать глубже - строении клеток, хромосом и генов, а далее - в возникновении самой жизни на Земле.

Заключение

Математик и Козлик

Делили пирог.

Козлик скромно сказал:

– Раздели его вдоль!

– Тривиально!– сказал Математик.–

Позволь,

Я уж лучше

Его разделю поперек!…

Льюис Кэрролл.Приключения Алисы в стране Чудес. В пересказе Б.Заходера.

Природа, понимаемая как весь мир в многообразии его форм, состоит как бы из двух частей: живая и неживая природа. Для творений неживой природы характерна высокая устойчивость, слабая изменчивость, если судить в масштабах человеческой жизни. Человек рождается, живет, стареет, умирает, а гранитные горы остаются такими же и планеты вращаются вокруг Солнца так же, как и во времена Пифагора.

Мир живой природы предстает перед нами совсем иным - подвижным, изменчивым и удивительно разнообразным. Жизнь демонстрирует нам фантастический карнавал разнообразия и неповторимости творческих комбинаций! Мир неживой природы - это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир природы - это прежде всего мир гармонии, в которой действует "закон золотого сечения".

В современном мире наука приобретает особое значение в связи с усилением воздействия человека на природу. Важными задачами на современном этапе являются поиск новых путей сосуществование человека и природы, изучение философских, социальных, экономических, образовательных и других проблем, стоящих перед обществом.

В данной работе было рассмотрено влияние свойств «золотого сечения» на живую и не живую природу, на исторический ход развития истории человечества и планеты в целом. Анализируя все вышеизложенное можно еще раз подивиться грандиозности процесса познания мира, открытием все новых его закономерностей и сделать вывод: принцип золотого сечения – высшее проявление структурного и функциональгого совершенства целого и его частей в искусстве, науке, технике и природе. Можно ожидать, что законы развития различных систем природы, законы роста не очень разнообразны и прослеживаются в самых различных образованьях. В этом и проявляется единство природы. Идея такого единства, основанная на проявлении одних и тех же закономерностей в разнородных явлениях природы, сохранила свою актуальность от Пифагора до наших дней. При преподавании школьных предметов имеется возможность продемонстрировать взаимосвязи между понятиями, принятыми в различных областях знаний, и процессами , протекающими в природной среде, в человеческом обществе на примере свойств «золотого сечения». При изучении пропорций, прямоугольных треугольников, теоремы Пифагора, прямоугольников и правильных пятиугольников имеется возможность для ознакомления с понятием золотого сечения. Одновременно с этим может быть найден подход к созданию целостной картины мира в сознании школьников.

Приложение 1

Программа, вычисляющая значение j :

5 REM ‘ПРОГРАММА ВЫЧИСЛЕНИЯ ЗОЛОТОГО СЕЧЕНИЯ МЕТОДОМ ПРИБЛИЖЕНИЯ

10 Q#=1

20 FOR I=1 TO 24

30 Q#=1+1/Q#

40 PRINT I, Q#

50 NEXT I

60 END

В результате выполнения этой программы выдаются на экран монитора числа, которые постепенно сужаясь, подбираются к числу j:

1 2

2 1.5

3 1.666666666666667

4 1.6

5 1.625

6 1.615384615384615

7 1.619047619047619

8 1.617647058823529

9 1.618181818181818

10 1.617977528089888

11 1.618055555555556

12 1.618025751072961

13 1.618037135278515

14 1.618032786885246

15 1.618034447821682

16 1.618033813400125

17 1.618034055727554

18 1.618033963166707

19 1.618033998521803

20 1.618033985017358

21 1.618033990175597

22 1.618033988205325

23 1.618033988957902

24 1.618033988670443

Приложение 2

Приложение 3

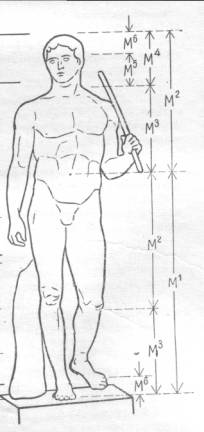
Рис. 11. Золотые пропорции в фигуре человека

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Приложение 4

Cтатуя Поликлетa 'Дорифор'

Cтатуя Агесандрa 'Афродита Милосская'

Список ключевых слов.

1. Базальт - темная эффузивная основная горная порода.

2. Бел - логарифмическая единица отношения двух величин (десятичный логарифм отношения двух одноименных физических величин, напр. мощностей, токов, звукового давления), обозначается бел.

3. Биоритмы - циклические колебания интенсивности и характера биологических процессов и явлений.

4. Бронзовый век - исторический период, сменивший энеолит и характеризующийся распространением металлургии бронзы, бронзовых орудий и оружия в кон. 4 — нач. 1-го тыс. до н. э.

5. Габбаро - (итал. gabbro), интрузивная основная глубинная горная порода.

6. Гармония - (греч. harmonia — связь, стройность, соразмерность), соразмерность частей, слияние различных компонентов объекта в единое органическое целое.

7. Геометрия - (от гео... и ...метрия), раздел математики, в котором изучаются пространственные отношения (напр., взаимное расположение) и формы (напр., геометрические тела) и их обобщения.

8. Гранит(итал. granito, букв. — зернистый)- наиболее распространенная в земной коре континентов кислая полнокристаллическая магматическая горная порода.

9. Децибел - десятая часть бела, обозначается дБ.

10. Диастолическое давление - минимальное артериальное кровяное давление в период диастолы сердца; определяется с помощью сфигмоманометра и стетоскопа.

11. Дискретность (от лат. discretus — разделенный, прерывистый) - прерывность; противопоставляется непрерывности

12. Додекаэдр(от греч. dodeka — двенадцать и hedra — грань) - один из пяти типов правильных многогранников; имеет 12 граней (пятиугольных), 30 ребер, 20 вершин (в каждой сходятся 3 ребра).

13. Железный век - период в развитии человечества, наступивший с распространением металлургии железа и изготовлением железных орудий и оружия. Сменил бронзовый век в основном в нач. 1-го тыс. до н. э.

14. Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.

15. Иррациональное число - число, не являющееся рациональным, т. е. не могущее быть точно выраженным дробью m/n, где m и n — целые числа.

16. Логарифмическая спираль - плоская кривая, описываемая точкой, движущейся по прямой, которая вращается около одной из своих точек О (полюса логарифмической спирали) так, что логарифм расстояния движущейся точки от полюса изменяется пропорционально углу поворота; логарифмическая спираль пересекает под постоянным углом a все прямые, выходящие из полюса.

17. Магма (от греч. magma — густая мазь)- расплавленная масса преимущественно силикатного состава, образующаяся в глубинных зонах Земли.

18. Мезолит (от мезо... и ...лит) - средний каменный век, переход от палеолита к неолиту (ок. 10-го — 5-е тыс. до н. э.).

19. Неолит (от нео... и ...лит) - новый каменный век, период (ок. 8 — 3-го тыс. до н. э.) перехода от присваивающего хозяйства (собирательство, охота) к производящему (земледелие, скотоводство).

20. Палеолит (от палео... и ...лит) - древний каменный век, первый период каменного века, время существования ископаемого человека

21. Пентаграмма (греч. pentagrammon, от pente — пять и gramma — линия) - правильный пятиугольник, на каждой стороне которого построены равнобедренные треугольники, равные по высоте. В средние века — распространенный магический знак.

22. Пропорция - (лат. proportio), в математике равенство между двумя отношениями четырех величин: a/ b = c/ d.

23. Сегмент - лат. segmentum, от seco — рассекаю),
1) часть круга, ограниченная дугой и ее хордой.
2) То же, что отрезок

24. Симметрия (от греч. symmetria — соразмерность) - в широком смысле — инвариантность (неизменность) структуры, свойств, формы материального объекта относительно его преобразований (т. е. изменений ряда физических условий). Симметрия лежит в основе законов сохранения

25. Система - (от греч. sysntema — целое, составленное из частей; соединение), множество элементов, находящихся в отношениях и связях друг с другом, образующих определенную целостность, единство.

26. Систолическое давление - артериальное давление в момент максимального подъема пульсовой волны вслед за систолой левого желудочка сердца.

27. Спирали - (от греч. speira — виток), кривые, закручивающиеся вокруг точки на плоскости

28. Филотаксис - строгий математический характер винтового расположения листьев на стебле растения.

29. Хронология - последовательность исторических событий во времени.

30. Числа «Фибоначчи» - последовательность чисел, особенность которых состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих.

31. Эволюция - представление об изменениях в обществе и природе, их направленности, порядке, закономерностях; определяет состояние какой-либо системы рассматривается как результат более или менее длительных изменений ее предшествовавшего состояния;

Построение «золотого» прямоугольника:

Месяцы

2.2.Последовательность Фибоначчи и хронология древнейшей истории.